Рычаги в физике формулы

Рычаги в физике формулы

Сила человека ограничена. Поэтому он часто применяет устройства (или приспособления), позволяющие преобразовать его силу в силу, существенно большую. Примером подобного приспособления является рычаг.

Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры. В качестве рычага могут быть использованы лом, доска и тому подобные предметы.

Различают два вида рычагов. У рычага 1-го рода неподвижная точка опоры O располагается между линиями действия приложенных сил (рис. 47), а у рычага 2-го рода она располагается по одну сторону от них (рис. 48).

Использование рычага позволяет получить выигрыш в силе. Так, например, рабочий, изображенный на рисунке 47, прикладывая к рычагу силу 400 Н, сможет приподнять груз весом 800 Н.

Разделив 800 Н на 400 Н, мы получим выигрыш в силе, равный 2.

Для расчета выигрыша в силе, получаемого с помощью рычага, следует знать правило, открытое Архимедом еще в III в. до н. э. Для установления этого правила проделаем опыт. Укрепим на штативе рычаг и по обе стороны от оси вращения прикрепим к нему грузы (рис. 49).

Действующие на рычаг силы F1 и F2 будут равны весам этих грузов. Из опыта, изображенного на рисунке 49, видно, что если плечо одной силы (т. е.

расстояние OA ) в 2 раза превышает плечо другой силы (расстояние OB ), то силой 2 Н можно уравновесить в 2 раза большую силу – 4 Н. Итак, для того чтобы уравновесить меньшей силой большую силу, необходимо, чтобы ее плечо превышало плечо большей силы.

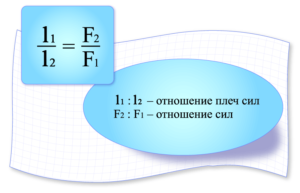
Обозначим плечи сил через l1 и l2 (рис. 50). Тогда правило рычага можно представить в виде следующей формулы:

(20.1)

Эта формула показывает, что рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам.

Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте (рис. 51). Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту 147 м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу 2,5 т!

Интересное:  Если беременная заболела к какому врачу идти

В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы и т. д.).

1. Что представляет собой рычаг? 2. В чем заключается правило рычага? Кто его открыл? 3. Чем отличается рычаг 1-го рода от рычага 2-го рода? 4. Приведите примеры применения рычагов. 5. Рассмотрите рисунки 52, а и 52, б. В каком случае груз нести легче? Почему?

Экспериментальное задание. Положите под середину линейки карандаш так, чтобы линейка находилась в равновесии. Не меняя взаимного расположения линейки и карандаша, уравновесьте иа полученном рычаге одну монету с одной стороны и стопку из трех таких же монет с другой стороны. Измерьте плечи приложенных (со стороны монет) сил и проверьте правило рычага.

Рычаг — это твердое тело, вращающееся вокруг некоторой оси. Различают Одноплечный рычаг и Двуплечный прямой рычаг и Двуплечный угловой рычаг.

У одноплечного рычага ось расположена на одном из его концов, а силы действующие на него, параллельны но направлены в противоположные стороны (антипараллельны).

У двуплечного прямого рычага ось расположена между точками приложения сил, а силы параллельны и имеют одинаковое направление.

Во всех случаях длины плечей находятся, как расстояния от оси вращения до линий действия силы по перпендикуляру.

Правило Рычага

Сила · Плечо силы = Нагрузка · Плечо нагрузки

То, используя правило рычага получим:

Простые механизмы: рычаг, равновесие сил на рычаге

С самых давних пор человек применяет различные вспомогательные приспособления для облегчения своего труда. Как часто, когда нам надо сдвинуть с места очень тяжелый предмет, мы берем себе в помощники палку или шест. Это пример простого механизма – рычага.

Применение простых механизмов

Видов простых механизмов очень много. Это и рычаг, и блок, и клин, и многие другие. Простыми механизмами в физике называют приспособления, служащие для преобразования силы.

Наклонная плоскость, которая помогает вкатывать или втаскивать тяжелые предметы наверх – это тоже простой механизм. Применение простых механизмов очень распространено как в производстве, так и в быту.

Чаще всего простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить в несколько раз силу, действующую на тело.

Интересное:  Беременность не показывает на узи

Рычаг в физике — простой механизм

Один из самых простых и распространенных механизмов, который изучают в физике еще в седьмом классе – рычаг. Рычагом в физике называют твердое тело, способное вращаться вокруг неподвижной опоры.

Различают два вида рычагов. У рычага первого рода точка опоры находится между линиями действия приложенных сил. У рычага второго рода точка опоры расположена по одну сторону от них.

То есть, если мы пытаемся при помощи лома сдвинуть с места тяжелый предмет, то рычаг первого рода – это ситуация, когда мы подкладываем брусок под лом, надавливая на свободный конец лома вниз. Неподвижной опорой у нас в данном случае будет являться брусок, а приложенные силы располагаются по обе стороны от него.

А рычаг второго рода – это когда мы, подсунув край лома под тяжесть, тянем лом вверх, пытаясь таким образом перевернуть предмет. Здесь точка опоры находится в месте упора лома о землю, а приложенные силы расположены по одну сторону от точки опоры.

Закон равновесия сил на рычаге

Используя рычаг, мы можем получить выигрыш в силе и поднять неподъемный голыми руками груз. Расстояние от точки опоры до точки приложения силы называют плечом силы. Причем, можно рассчитать равновесие сил на рычаге по следующей формуле:

где F1 и F2 – силы, действующие на рычаг,

а l2 и l1 – плечи этих сил.

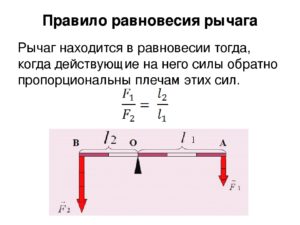
Это и есть закон равновесия рычага, который гласит: рычаг находится в равновесии тогда, когда действующие на него силы обратно пропорциональны плечам этих сил.

Этот закон был установлен Архимедом еще в третьем веке до нашей эры. Из него следует, что меньшей силой можно уравновесить большую. Для этого необходимо, чтобы плечо меньшей силы было больше плеча большей силы.

А выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил.

Начав использоваться с глубокой древности, рычаг повсеместно применяется и в наши дни, как на производстве, например, подъемные краны, так и в быту, например, ножницы, весы и так далее.

Источники: http://phscs.ru/physics7/leverhttp://www.fxyz.

ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0/%D1%81%D1%82%D0%B0%D1%82%D0%B8%D0%BA%D0%B0/%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%8B%D0%B5_%D0%BC%D0%B0%D1%88%D0%B8%D0%BD%D1%8B/%D1%80%D1%8B%D1%87%D0%B0%D0%B3/http://www.nado5.ru/e-book/prostye-mekhanizmy-rychag

Источник: https://rojaismelo.ru/privivki-rebenku/rychagi-v-fizike-formuly

Формула плеча силы

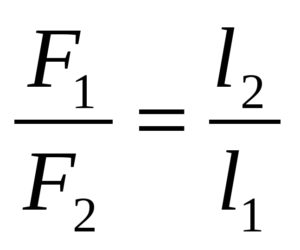
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${\overline{F}}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $\left|OA\right|=d_1$- плечо силы $F_1$; $\left|OA\right|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $\overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($\varepsilon $) точки определяется тангенциальной составляющей ($F_{\tau }$) силы $\overline{F}$:

\[mR\varepsilon =F_{\tau }\left(2\right),\]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{\tau }$ — проекция силы на направление скорости движения точки.

Если угол $\alpha $ — это угол между вектором силы $\overline{F}$ и радиус — вектором $\overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

\[F_{\tau }=F{\sin \alpha \ \left(3\right).\ }\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

\[d=R{\sin \alpha \ \left(4\right).\ }\]

Если на точку будет действовать сила ($\overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $\alpha $ станет равен $\frac{\pi }{2}$.

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$. Модуль вектора момента силы равен:

\[M=F{r\sin \alpha =\ }Fd\ \left(6\right).\]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз).

При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Пример 1

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={\rm 2\ }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

Решение. Основой решения задачи является правило равновесия рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1.1\right),\]

где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:

\[\frac{m_1g}{m_2g}=\frac{d_2}{d_1}\to \frac{m_1}{m_2}=\frac{d_2}{d_1}\left(1.2\right).\]

Из выражения (1.2) получим искомую массу $m_1$:

\[m_1=\frac{m_2d_2}{d_1}.\]

Вычислим искомую массу:

\[m_1=2\cdot \frac{1}{4}=0,5\ (кг).\]

Ответ. $m_1=0,5\ кг$

Пример 2

Задание. Однородный стержень длинной $l\ $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $\alpha $. На стержне на расстоянии $b\ $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $M\overline{g}$, вес груза, расположенного на нем $\overline{P}=m_1\overline{g}$, сила реакции наклонной плоскости: $\overline{N}$; сила реакции опоры в точке A: $\overline{N}'$.

Плечи сил будем искать относительно точки A. Плечо силы $\overline{N'}$ будет равно нулю, так как сила приложена к стержню в точке А:

\[d_{N'}=0\ \left(2.1\right).\]

Плечо другой силы реакции опоры ($\overline{N}$) равно длине перпендикуляра AC:

\[d_N=l{\sin (90-\alpha )\ }=l{\cos \alpha \ \left(2.2\right).\ }\]

Плечо силы $M\overline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

\[d_{Mg}=\frac{l}{2}\left(2.3\right).\] Плечо силы $m_1\overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
\[d_{m_1g}=b.\]

Ответ. $d_{N'}=0;;\ d_N=l{sin (90-\alpha )\ }=l{cos \alpha \ \left(м\right),\ }d_{Mg}=\frac{l}{2},\ d_{m_1g}=b$

Читать дальше: формула полезной мощности.

}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.»,»word_count»:616,»direction»:»ltr»,»total_pages»:1,»rendered_pages»:1}

Источник: https://www.webmath.ru/poleznoe/fizika/fizika_137_formula_plecha_sily.php

Простые механизмы. КПД простых механизмов – FIZI4KA

ОГЭ 2018 по физике ›

1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.

Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.

2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага.

К одному концу рычага подвешен груз, действующий на рычаг с силой ​\( F_1 \)​, равной весу груза. Действуя на длинный конец рычага с силой ​\( F_2 \)​, человек поднимает груз.

При этом сила \( F_1 \)​ стремится повернуть рычаг по часовой стрелке, а груз \( F_2 \) — против часовой стрелки.

Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы ​\( F_1 \)​ является расстояние ОА ​\( (l_1) \)​, плечом силы \( F_2 \) — расстояние ОВ \( (l_2) \).

Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. ​\( F_1l_1=F_2l_2 \)​. Произведение силы, действующей на рычаг, и её плеча называют моментом силы: ​\( Fl=M \)​. Соответственно, если рычаг находится в равновесии, то ​\( M_1=M_2 \)​.

Условие равновесия рычага можно записать по-другому:​\( \frac{F_1}{F_2}=\frac{l_2}{l_1} \)​. Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.

Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.

3. При подъеме груза работа силы, действующей на груз, равна ​\( A_1=F_1h_1 \)​, работа силы, приложенной к другому концу рычага, равна \( A_2=F_2h_2 \).

Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и ​\( \frac{AO}{BO}=\frac{AC}{BD} \)​ или ​\( \frac{l_1}{l_2}=\frac{h_1}{h_2} \).​ Поскольку ​\( F_1l_1=F_2l_2 \)​, то ​\( F_1h_1=F_2h_2 \)​, т.е. ​\( A_1=2 \)​.

Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.

4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).

Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.

Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB.

В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: ​\( P=F \)​.

Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.

Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.

В этом случае точкой вращения блока является точка А (см. рис. 52).

Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: ​\( P=2F \)​. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: ​\( F=P/2 \)​.

5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).

Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик.

Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу ​\( P \)​. Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную ​\( F=P\sin\alpha \)​, т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии.

Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх.

В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости.

Он равен отношению полезной работы ко всей совершённой работе: ​\( \mathbf{КПД}=A_п/A_с\cdot 100 \% \)​, где ​\( A_п \)​ — полезная работа, ​\( A_п=mgh \)​; ​\( A_с \)​ — совершённая работа при перемещении ящика вдоль наклонной плоскости, ​\( A_c=Fl \)​, где ​\( F \)​ — приложенная сила, ​\( l \)​ — длина наклонной плоскости.

• Примеры заданий
• Ответы

Часть 1

1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо ​\( l_1 \)​?

1) 12,8 м 2) 2,5 м 3) 0,8 м

4) 0,25 м

2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.

Чему равна сила ​\( F_1 \)​, если рычаг находится в равновесии?

1) 100 Н 2) 50 Н 3) 25 Н

4) 9 Н

3. Рычаг находится в равновесии под действием двух сил. Сила ​\( F_1 \)​ = 6 Н. Чему равна сила \( F_2 \), если длина рычага 50 см, а плечо силы \( F_1 \) равно 30 см?

1) 0,1 Н 2) 3,6 Н 3) 9 Н

4) 12 Н

4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью

1) подвижного блока 2) неподвижного блока 3) рычага

4) наклонной плоскости

5. С помощью неподвижного блока в отсутствие трения силе

1) выигрывают в 2 раза 2) не выигрывают, но и не проигрывают 3) проигрывают в 2 раза

4) возможен и выигрыш, и проигрыш

6. С помощью подвижного блока в отсутствие трения

1) выигрывают в работе в 2 раза 2) проигрывают в силе в 2 раза 3) не выигрывают в силе

4) выигрывают в силе в 2 раза

7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна

1) 4 кг 2) 2 кг 3) 0,5 кг

4) 1 кг

8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость

1) даёт выигрыш в 2 раза 2) даёт выигрыш в 4 раза 3) не даёт ни выигрыша, ни проигрыша

4) даёт проигрыш в 2 раза

9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?

1) 1,25 м 2) 2 м 3) 12,5 м

4) 20 м

10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?

1) 160% 2) 62,5% 3) 16%

4) 6,25%

11. Груз поднимают с помощью подвижного блока радиусом ​\( R \)​ (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы ​\( \vec{F}_1 \)​ относительно точки A
Б) плечо силы \( \vec{F}_2 \) относительно точки A
B) момент силы \( \vec{F}_1 \) относительно точки A

ФОРМУЛЫ
1) ​\( F_1R \)​
2) \( 2F_1R \)
3) \( \frac{F_1}{R} \)
4) ​\( R \)​
5) ​\( 2R \)​

12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Любой простой механизм даёт выигрыш в силе. 2) Ни один простой механизм не даёт выигрыша в работе. 3) Наклонная плоскость выигрыша в силе не даёт. 4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.

5) Неподвижный блок даёт выигрыш в силе в 2 раза.

Часть 2

13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.

Ответы

Источник: https://fizi4ka.ru/ogje-2018-po-fizike/prostye-mehanizmy-kpd-prostyh-mehanizmov.html

Правило рычага. Формулировка и формула

Рычаг представляет собой один из простых механизмов, который служил и продолжает служить людям для облегчения их физического труда. В статье рассмотрим, что такое рычаг, какие виды его бывают и где они применяются, а также поясним, в чем заключается правило рычага.

Рычаг в физике

Несмотря на то что речь идет о простом механизме, он все же имеет свои составные части. Во-первых, это балка или доска, которая предназначена для воздействия на нее двух противоположных сил.

Во-вторых, это опора, которая, с геометрической точки зрения, представляет собой ось вращения, вокруг которой может двигаться балка.

В зависимости от расположения опоры под балкой различают три типа рычага, которые будут рассмотрены ниже.

Еще одним важным понятием для любого рычага является «плечо». Под ним понимают часть балки, которая находится между ее концом и опорой при условии, что воздействующие силы приложены к концам балки. Длина плеча играет важную роль при определении условий равновесия рычага.

Рычаг предназначен для преобразования силы в перемещение или, наоборот, перемещения в силу. Другими словами, рассматриваемый простой механизм, используется для перераспределения работы, которую следует выполнить, в пользу приложенной силы или в пользу осуществляемого перемещения. Рисунок ниже показывает пример рычага первого рода.

Когда человечество начало использовать рычаг?

Ответить уверенно на этот вопрос нельзя. Известно, что рычаги с древнейших времен использовались в Месопотамии и Древнем Египте для подъема тар с водой из колодцев и рек.

Единственным письменным свидетельством, которое сохранилось до наших дней, свидетельствующим об использовании рассматриваемого механизма, является всем известный рычаг Архимеда. В работе Плутарха «Параллельные жизни» (100 год до н. э.) говорится, что Архимед в одиночку смог поднять корабль с грузом и пассажирами над поверхностью воды. При этом философ использовал систему блоков и рычагов.

Если подойти к поставленному в названии пункта вопросу более строго, то можно сказать, что человек пользуется рычагом с момента собственного появления в этом мире, ведь наши предплечья и плечи работают по принципу этого простого механизма.

Понятие о моменте силы

Прежде чем переходить к формулировке правила равновесия рычага, рассмотрим понятие крутящего момента или момента силы. В физике под ним понимают величину, равную произведению плеча силы на саму силу. Математически это записывается так:

M = d*F.

Где, F — воздействующая сила, d — плечо силы, которое соответствует расстоянию от точки приложения F до оси вращения. Последний элемент системы, то есть ось вращения, играет принципиальную роль при определении момента M. Без наличия оси вращения нет никакого смысла говорить о действующем моменте силы.

Физический смысл величины M заключается в отражении способности силы F совершить поворот системы вокруг оси. На практике эту способность можно ощутить, если попытаться открутить гайку не гаечным ключом, а руками, или же если постараться открыть дверь не за ручку, а толкая ее вблизи навесных петель.

Во время решения задач момент силы M может приводить как к вращению системы по часовой стрелке, так и против ее хода. В первой случае момент считают отрицательным, во втором — положительным.

Моменты сил и правило рычага

Рассмотрим классический рычаг с двумя плечами, когда опора находится вдали от концов балки. Пример такого механизма изображен ниже.

Мы видим, что когда этот рычаг применяют для совершения физической работы, то на него действует две силы:

• внешняя сила F, которую прикладывают для выполнения полезной работы;
• сила R, которая оказывает сопротивление силе F (она выполняет отрицательную работу).

В большинстве случаев сила F создается усилием человека, а сила R представляет собой вес некоторого груза.

Рассматриваемый рычаг будет находиться в равновесии, и перестанет испытывать вращение только тогда, когда сумма действующих на него моментов будет равна нулю. Используя обозначения рисунка выше, и применяя формулу для M, запишем правило равновесия рычага:

R*dR — F*dF = 0.

Заметим, что момент силы F записан со знаком минус, поскольку он стремится повернуть плечо рычага по часовой стрелке. Остается перенести второй член в правую часть равенства, чтобы записать правило рычага:

R*dR = F*dF.

Кто установил правило равновесия рычага? Этот вопрос отчасти пересекается с рассмотренным выше историческим. Поскольку сохранились только письменные свидетельства научной деятельности Архимеда, связанной с этим механизмом, то именно он в настоящее время считается тем философом, кто установил правило рычага.

Равновесие рассматриваемой системы обеспечивается не только равенством нулю суммы моментов, но также равенством нулю всех действующих сил. Выше были названы лишь две силы (F и R). На самом же деле существует еще сила реакции опоры, направленная против сил F и R. Реакцию опоры момента силы не создает ввиду нулевой длины ее плеча.

Выигрыш и проигрыш в использовании рычага

Следует четко понимать, что при использовании рычага сохраняется полная энергия системы. Чтобы поднять груз на некоторую высоту, необходимо совершить определенную работу.

Поскольку в формуле правила рычага стоит произведение силы на длину плеча, то отмеченную работу можно выполнить как с помощью большей силы, так и с помощью меньшей.

Однако в первом случае необходимо будет переместить плечо рычага в вертикальном направлении на малую величину, во втором же случае — на большую величину. Это и есть выигрыш и проигрыш в использовании рычага.

Заметим, что в формуле правила рычага стоят значения моментов. Никакого отношения к работе они не имеют. Момент силы выполняет работу только тогда, когда система за счет его действия поворачивается вокруг оси на некоторый угол.

Виды рычагов

Выше уже упоминалось, что все рычаги относятся к одному из трех типов. В основе классификации лежит относительное расположение сил R, F и опоры. Охарактеризуем все три типа:

1. Рычаг 1-го типа, или рода, был показан выше. Опора расположена в нем между силами R и F. В зависимости от длины плеч dR и dF его можно использовать как для выигрыша в пути, так и для выигрыша в силе. Примером этого типа рычага являются ножницы, весы, гвоздодер.
2. Рычаг 2-го рода предполагает, что сила R приложена между опорой и силой F. В таком случае получается выигрыш только в силе. Примерами таких рычагов в быту являются орехокол или ручная тачка.
3. Рычаг 3-го рода предполагает, что сила F расположена между опорой и грузом R. В этом случае выигрыш возможен только в пути. Использование лопаты, циркуля или удочки для рыбалки — это яркие примеры рычага 3-го рода в работе.

Простой механизм блок

Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме — блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.

Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.

Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.

Решение задачи

Ручная тачка сделана таким образом, что центр массы груза в ней находится на расстоянии 1/3*l от колеса, где l — длина тачки. Какой массы груз может переместить с помощью тачки человек, если известно, что он может приложить максимальную вертикальную силу F = 200 Н.

Воспользуемся правилом рычага, получим:

F*l = R*1/3*l

F = m*g/3

m = 3*F/g = 3*200/9,81 ≈ 61 кг.

Отметим, что сила F = 200 Н равна весу тела массой всего 20,4 кг. Таким образом, данная ручная тачка позволяет выиграть в 3 раза в силе.

Источник: https://FB.ru/article/451673/pravilo-ryichaga-formulirovka-i-formula

Простые механизмы. Рычаги. Момент силы. Физика. 7 класс. — Объяснение нового материала

Объяснение нового материала. Простые механизмы. Рычаги. Момент силы.

В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы.

Среди них древнейшие изобретения человечества: блок и рычаг.

Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.

Блок — это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке. Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.

Подвижный и неподвижный блок — такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.

Неподвижный блок Архимед рассматривал как равноплечий рычаг. Момент силы, действующей с одной стороны блока, равен моменту силы, приложенной с другой стороны блока. Одинаковы и силы, создающие эти моменты.

Подвижный блок Архимед принимал за неравноплечий рычаг, дающий выигрыш в силе в 2 раза. Относительно центра вращения действуют моменты сил, которые при равновесии должны быть равны.
Архимед изучил механические свойства подвижного блока и применил его на практике.

По свидетельству Афинея, «для спуска на воду исполинского корабля, построенного сиракузским тираном Гиероном, придумывали много способов, но механик Архимед, применив простые механизмы, один сумел сдвинуть корабль с помощью немногих людей.

Архимед придумал блок и посредством него спустил на воду громадный корабль».

Блок не дает выигрыша в работе, подтверждая «золотое правило» механики. В этом легко убедиться, обратив внимание на расстояния, пройденные рукой и гирей.

Спортивные парусные суда, как и парусники прошлого, не могут обойтись без блоков при постановке парусов и управлении ими. Современным судам нужны блоки для подъема сигналов, шлюпок.

Эта комбинация подвижных и неподвижных блоков на линии электрофицированной железной дороги для регулировки натяжения проводов.

Такой системой блоков могут пользоваться планеристы для подъема в воздух своих аппаратов.

ВОРОТ

Это два колеса, соединенные вместе и вращающиеся вокруг одной оси, например, колодезный ворот с ручкой.

Ворот можно рассматривать как неравноплечий рычаг: выигрыш в силе, даваемый им, зависит от соотношения радиусов R и r.

ЛЕБЁДКА

Лебедка — конструкция , состоящая из двух воротов с промежуточными передачами в механизме привода.

Грузоподъемность современных лебедок может быть свыше 100 кН. Они работают на канатных дорогах, на буровых установках, выполняют строительно-монтажные и погрузочно-разгрузочные работы.

Лебедка с двигателем внутреннего сгорания.

Электрическая передвижная лебедка.

ЗУБЧАТАЯ ПЕРЕДАЧА

— система находящихся в зацеплении зубчатых колес ( шестеренок) в какой-то мере аналогична вороту.

НАКЛОННАЯ ПЛОСКОСТЬ

Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия. К таким устройствам относятся пандусы, эскалаторы, обычные лестницы и конвейеры.

Если нужно поднять груз на высоту, всегда легче воспользоваться пологим подъемом, чем крутым. Причем, чем положе уклон, тем легче выполнить эту работу. Когда время и расстояние не имеют большого значения , а важно поднять груз с наименьшим усилием, наклонная плоскость оказывается незаменима.

С помощью этих рисунков можно объяснить, как работает простой механизм НАКЛОННАЯ ПЛОСКОСТЬ.
Классические расчеты действия наклонной плоскости и других простых механизмов принадлежат выдающемуся античному механику Архимеду из Сиракуз.

При строительстве храмов египтяне транспортировали, поднимали и устанавливали колоссальные обелиски и статуи, вес которых составлял десятки и сотни тонн! Все это можно было сделать, используя среди других простых механизмов наклонную плоскость. Главным подъемным приспособлением египтян была наклонная плоскость — рампа.

Угол наклона рампы был очень незначительным — 5 или 6 градусов.

Колонны древнего египетского храма в Фивах.

Каждую из этих огромных колонн рабы втаскивали по рампе- наклонной плоскости. Когда колонна вползала в яму, через лаз выгребали песок, а затем разбирали кирпичную стенку и убирали насыпь. Таким образом, например, наклонная дорога к пирамиде Хафра при высоте подъема в 46 метров имела длину около полукилометра.

«Тело на наклонной плоскости удерживается силой, которая … по величине во столько раз меньше веса этого тела, во сколько раз длина наклонной плоскости больше ее высоты».
Это условие равновесия сил на наклонной плоскости сформулировал голландский ученый Симон Стевин (1548-1620).

Рисунок на титульном листе книги С. Стевина, которым он подтверждает свою формулировку.

Очень остроумно использована наклонная плоскость на Красноярской ГЭС. Здесь вместо шлюзов действует судовозная камера, движущаяся по наклонной эстакаде. Для ее передвижения необходимо тяговое усилие в 4000 кН.

А почему горные дороги вьются пологим «серпантином»?

КЛИН

Клин — одна из разновидностей простого механизма под названием «наклонная плоскость». Клин состоит из двух наклонных плоскостей, основания которых соприкасаются. Его применяют, чтобы получить выигрыш в силе, то есть при помощи меньшей силы противодействовать большей силе. При рубке дров, чтобы облегчить работу, в трещину полена вставляют металлический клин и бьют по нему обухом топора.

Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце .Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения.

ВИНТ

Другой разновидностью наклонной плоскости является винт. Винт — наклонная плоскость, навитая на ось. Резьба винта – это наклонная плоскость, многократно обернутая вокруг цилиндра.

Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце. Реальный выигрыш клина определить трудно. Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения.

Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.

Момент силы

Условием равновесия рычага F1/F2 = l2/l1 можно пользоваться, если к рычагу приложены только две силы.

А каково условие равновесия рычага в случае, когда к рычагу приложено несколько сил?

Чтобы найти это условие, перепишем равенство F1/F2 = l2/l1 в виде F1l1 = F2l2. Теперь величины, характеризующие силу, стремящуюся вращать рычаг в одном направлении, находятся в одной части равенства, а величины, характеризующие силу, стремящуюся вращать рычаг в противоположном направлении, — в другой части равенства.

Произведение модуля силы на ее плечо называют моментом силы: М = FI. Момент первой силы M1 = F1l1 а момент второй силы М2 = F2l2. Поэтому условие F1l1 = F2l2 можно переписать теперь в виде М1 = М2.

С использованием понятия момента силы условие равновесия рычага можно сформулировать так: рычаг находится в равновесии, если момент силы, стремящейся вращать рычаг в одном направлении, равен моменту силы, стремящейся вращать его в противоположном направлении.

Опыт и расчет показывают, что это справедливо и тогда, когда к рычагу приложено несколько сил: рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении.

Условие равновесия рычага в таком виде называют правилом моментов. Приведем пример использования этого правила.

Решим задачу

Какой массы груз надо подвесить в точке А (рис. 25.5, а), чтобы рычаг находился в равновесии? Масса каждого груза равна 100 г, расстояние между соседними штрихами на рычаге равно 10 см.

Рис. 25.5. К решению задачи

Ответ: 0,4 кг.

Домашнее задание

Задание 1. Ответь на вопросы.

1. Что такое рычаг? Приведите примеры рычага.
2. Что такое плечо силы?
3. Сформулируйте условие равновесия рычага.
4. Как с помощью рычага получить выигрыш в пути? Приведите примеры такого использования рычага.
5. Что такое момент силы? Сформулируйте правило моментов.

Задание 2. Реши ребус.

К занятию прикреплен файл  «!». Вы можете скачать файл в любое удобное для вас время.

Использованные источники: http://www.tepka.ru/fizika_7  , http://class-fizika.narod.ru
 

Источник: https://www.kursoteka.ru/course/2755/lesson