Расчет усилия на рычаге

Правило рычага. Формулировка и формула

Рычаг представляет собой один из простых механизмов, который служил и продолжает служить людям для облегчения их физического труда. В статье рассмотрим, что такое рычаг, какие виды его бывают и где они применяются, а также поясним, в чем заключается правило рычага.

Рычаг в физике

Несмотря на то что речь идет о простом механизме, он все же имеет свои составные части. Во-первых, это балка или доска, которая предназначена для воздействия на нее двух противоположных сил.

Во-вторых, это опора, которая, с геометрической точки зрения, представляет собой ось вращения, вокруг которой может двигаться балка.

В зависимости от расположения опоры под балкой различают три типа рычага, которые будут рассмотрены ниже.

Рычаг предназначен для преобразования силы в перемещение или, наоборот, перемещения в силу. Другими словами, рассматриваемый простой механизм, используется для перераспределения работы, которую следует выполнить, в пользу приложенной силы или в пользу осуществляемого перемещения. Рисунок ниже показывает пример рычага первого рода.

Когда человечество начало использовать рычаг?

Ответить уверенно на этот вопрос нельзя. Известно, что рычаги с древнейших времен использовались в Месопотамии и Древнем Египте для подъема тар с водой из колодцев и рек.

Единственным письменным свидетельством, которое сохранилось до наших дней, свидетельствующим об использовании рассматриваемого механизма, является всем известный рычаг Архимеда. В работе Плутарха «Параллельные жизни» (100 год до н. э.) говорится, что Архимед в одиночку смог поднять корабль с грузом и пассажирами над поверхностью воды. При этом философ использовал систему блоков и рычагов.

Если подойти к поставленному в названии пункта вопросу более строго, то можно сказать, что человек пользуется рычагом с момента собственного появления в этом мире, ведь наши предплечья и плечи работают по принципу этого простого механизма.

Понятие о моменте силы

Прежде чем переходить к формулировке правила равновесия рычага, рассмотрим понятие крутящего момента или момента силы. В физике под ним понимают величину, равную произведению плеча силы на саму силу. Математически это записывается так:

M = d*F.

Где, F — воздействующая сила, d — плечо силы, которое соответствует расстоянию от точки приложения F до оси вращения. Последний элемент системы, то есть ось вращения, играет принципиальную роль при определении момента M. Без наличия оси вращения нет никакого смысла говорить о действующем моменте силы.

Физический смысл величины M заключается в отражении способности силы F совершить поворот системы вокруг оси. На практике эту способность можно ощутить, если попытаться открутить гайку не гаечным ключом, а руками, или же если постараться открыть дверь не за ручку, а толкая ее вблизи навесных петель.

Во время решения задач момент силы M может приводить как к вращению системы по часовой стрелке, так и против ее хода. В первой случае момент считают отрицательным, во втором — положительным.

Моменты сил и правило рычага

Рассмотрим классический рычаг с двумя плечами, когда опора находится вдали от концов балки. Пример такого механизма изображен ниже.

Мы видим, что когда этот рычаг применяют для совершения физической работы, то на него действует две силы:

• внешняя сила F, которую прикладывают для выполнения полезной работы;
• сила R, которая оказывает сопротивление силе F (она выполняет отрицательную работу).

В большинстве случаев сила F создается усилием человека, а сила R представляет собой вес некоторого груза.

Рассматриваемый рычаг будет находиться в равновесии, и перестанет испытывать вращение только тогда, когда сумма действующих на него моментов будет равна нулю. Используя обозначения рисунка выше, и применяя формулу для M, запишем правило равновесия рычага:

R*dR — F*dF = 0.

Заметим, что момент силы F записан со знаком минус, поскольку он стремится повернуть плечо рычага по часовой стрелке. Остается перенести второй член в правую часть равенства, чтобы записать правило рычага:

R*dR = F*dF.

Таким образом, равенство моментов силы действия F и силы противодействия R является достаточным условием равновесия рассматриваемого простого механизма.

Равновесие рассматриваемой системы обеспечивается не только равенством нулю суммы моментов, но также равенством нулю всех действующих сил. Выше были названы лишь две силы (F и R). На самом же деле существует еще сила реакции опоры, направленная против сил F и R. Реакцию опоры момента силы не создает ввиду нулевой длины ее плеча.

Выигрыш и проигрыш в использовании рычага

Следует четко понимать, что при использовании рычага сохраняется полная энергия системы. Чтобы поднять груз на некоторую высоту, необходимо совершить определенную работу.

Поскольку в формуле правила рычага стоит произведение силы на длину плеча, то отмеченную работу можно выполнить как с помощью большей силы, так и с помощью меньшей.

Однако в первом случае необходимо будет переместить плечо рычага в вертикальном направлении на малую величину, во втором же случае — на большую величину. Это и есть выигрыш и проигрыш в использовании рычага.

Заметим, что в формуле правила рычага стоят значения моментов. Никакого отношения к работе они не имеют. Момент силы выполняет работу только тогда, когда система за счет его действия поворачивается вокруг оси на некоторый угол.

Виды рычагов

Выше уже упоминалось, что все рычаги относятся к одному из трех типов. В основе классификации лежит относительное расположение сил R, F и опоры. Охарактеризуем все три типа:

1. Рычаг 1-го типа, или рода, был показан выше. Опора расположена в нем между силами R и F. В зависимости от длины плеч dR и dF его можно использовать как для выигрыша в пути, так и для выигрыша в силе. Примером этого типа рычага являются ножницы, весы, гвоздодер.
2. Рычаг 2-го рода предполагает, что сила R приложена между опорой и силой F. В таком случае получается выигрыш только в силе. Примерами таких рычагов в быту являются орехокол или ручная тачка.
3. Рычаг 3-го рода предполагает, что сила F расположена между опорой и грузом R. В этом случае выигрыш возможен только в пути. Использование лопаты, циркуля или удочки для рыбалки — это яркие примеры рычага 3-го рода в работе.

Простой механизм блок

Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме — блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.

Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.

Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.

Решение задачи

Ручная тачка сделана таким образом, что центр массы груза в ней находится на расстоянии 1/3*l от колеса, где l — длина тачки. Какой массы груз может переместить с помощью тачки человек, если известно, что он может приложить максимальную вертикальную силу F = 200 Н.

Воспользуемся правилом рычага, получим:

F*l = R*1/3*l

F = m*g/3

m = 3*F/g = 3*200/9,81 ≈ 61 кг.

Отметим, что сила F = 200 Н равна весу тела массой всего 20,4 кг. Таким образом, данная ручная тачка позволяет выиграть в 3 раза в силе.

Источник: https://FB.ru/article/451673/pravilo-ryichaga-formulirovka-i-formula

Расчет усилия на рычаге

Данный расчет позволяет рассчитать усилие развиваемое штоком пневмо или гидроцилиндра. Применение данного расчета позволяет мгновенно оценить с большой точностью усилия развиваемые штоком гидроцилиндра или пневмоцилиндра при работе.

Для расчета необходимо внести в соответствующие поля диаметр пневмоцилиндра или диаметр гидроцилиндра а также рабочее давление в системе сжатого воздуха или гидросистеме.

Выходными данными данного расчета является величина усилия развиваемая штоком пневмоцилиндра или гидроцилиндра.

D — Диаметр цилиндра;

S — Площадь поперечного сечения цилиндра;

P — Разница давлений;

F — Сила развиваемая системой;

Адрес: 426034г. Ижевск ул. Лихвинцева д. 70

Телефон/факс: +7 (3412) 230-210, 230-211, 230-212

Механический рычаг

С правилом рычага мы знакомы еще с курса школьной физики. Правило рычага основано на законе сохранения энергии, который звучит следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. Рассмотрим схему, показанную на рисунке:

На одном конце рычага, на расстоянии L1, расположен груз 1, создавая силу F1, на другом конце, на расстоянии L2, лежит груз 2, создавая силу F2.

Согласно закону сохранения энергии механическая энергия данной системы должна оставаться постоянной, т.е поэтому можно записать равенство:

где А — работа.

Для данной системы работу А1 и А2 можно определить, используя зависимости:

Приравняв указанные зависимости, получим:

Таким образом силу F2 можно определить так:

В данной зависимости соотношение длин рычагов L1 и L2 называют передаточным числом (или передаточным отношением).

Интересное:  Субпродукты с какого возраста детям

Показанный пример является самым простым видом рычага в механике, но другие, более сложные примеры, такие, как составной рычаг, основаны на тех же принципах и законах, что и обычный механический рычаг.

Калькулятор рычага

Калькулятор рычага. Передаточное отношение рычага =. Усилие: Нагрузка: Перемещение точки приложения усилия: Перемещение точки приложения нагрузки: Введите значения: — нагрузки, — плеча нагрузки, — плеча усилия, перемещения точки приложения нагрузки. Затем нажмите кнопку «Рассчитать».

‘ Листинг программы расчета рычага на языке Visual Basic Private Sub Calulate_Click() If ПлечоНагрузки > 0 And ПлечоУсилия > 0 Then N = ПлечоУсилия / ПлечоНагрузки Усилие = Нагрузка / N ПеремещениеУсилия = ПеремещениеНагрузки * N Else MsgBox («Плечи должны быть больше 0») End If End Sub.

Картинка 13 из презентации «Рычаг» к урокам физики на тему «Рычаг»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать картинку для урока физики, щёлкните по изображению правой кнопкой мышки и нажмите «Сохранить изображение как. ». Для показа картинок на уроке Вы также можете бесплатно скачать презентацию «Рычаг.ppt» целиком со всеми картинками в zip-архиве. Размер архива — 869 КБ.

«Простые механизмы» — Изобретения Архимеда. Наклонная плоскость. Блок. Проверь свои знания. Система блоков и тросов, предназначенная для повышения грузоподъемности. Архимед (около 287-212г. Рычаг,блок,наклонная плоскость,винт,клин. Винт. Блоки применяются в грузоподъемных устройствах. Расставь соответствующие названия простых механизмов изображенных на рисунках.

«Кинематическая схема» — Кинематическое исследование движения звеньев плоского механизма. Рассмотрим звено ОА. Длина звена AB = 60см. Длина DE = 40 см. Вектор скорости точки А перпендикулярен звену ОА. Расчетно-графическая работа №1. Вращательное движение. Длина кривошипа ОА = 30см. Масштаб. Расстояния О1D = CD = 30 см. Расстояние АС = 20 см.

«Рычаги в быту» — Наклонная плоскость. Равновесие рычага. При строительстве пирамид в Древнем Египте. Простые механизмы – приспособления, служащие для преобразования силы. Простые механизмы. Рычаг блок ворот. Механическая работа. Клин и винт. Рычаги в технике и быту: весы одночашечные рычажные. Рычаги в технике и быту: пресс с рычагом.

Интересное:  Роды с низкой плацентацией

«Исполнительный механизм» — Электродвигатель. Рабочий рычаг. Сердечник с клапаном. Входной фланец. Электрическая катушка. Устройство. Электрический ток. Ток в катушке не протекает. Электромагнитное реле — контактор. Пружина. Рабочее состояние. На катушку подается электрический ток. Выходной фланец. Силовые линии магнитного поля сердечника.

«Рычаг» — Исследовательская работа ученицы 4 «А» класса Шипиль Анны. Архимед, связав понятия силы, груза и плеча. У первого рычага длинное плечо в 3 раза больше короткого. Качели с перемещаемым сидением Подметальную машину. Перемещение точки приложения усилия: Нагрузка: Что такое рычаг? Груз. Легенда об Архимеде.

«Кулачковый механизм» — из Политехнического музея. Механический орган Павла Бруггера (Москва, 1880). Ручной привод машины. Основные тоны закрытых труб на октаву ниже открытых. Кулачковые механизмы. Язычковые трубы. Механический орган Бруггера. О памятниках науки и техники Политехнического музея. Самые распространенные — лабиальные трубы.

Источники: http://promtk.com/calc/pressurehttp://www.hydro-pnevmo.ru/topic.php?ID=8http://900igr.net/kartinki/fizika/Rychag/013-Kalkuljator-rychaga.html

Источник: https://rojaismelo.ru/privivki-rebenku/raschet-usiliya-na-rychage

Формула плеча силы

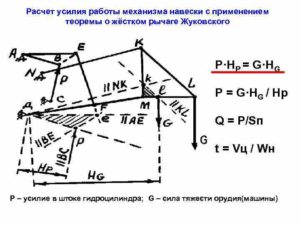
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${\overline{F}}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $\left|OA\right|=d_1$- плечо силы $F_1$; $\left|OA\right|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $\overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($\varepsilon $) точки определяется тангенциальной составляющей ($F_{\tau }$) силы $\overline{F}$:

\[mR\varepsilon =F_{\tau }\left(2\right),\]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{\tau }$ — проекция силы на направление скорости движения точки.

Если угол $\alpha $ — это угол между вектором силы $\overline{F}$ и радиус — вектором $\overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

\[F_{\tau }=F{\sin \alpha \ \left(3\right).\ }\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

\[d=R{\sin \alpha \ \left(4\right).\ }\]

Если на точку будет действовать сила ($\overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $\alpha $ станет равен $\frac{\pi }{2}$.

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$. Модуль вектора момента силы равен:

\[M=F{r\sin \alpha =\ }Fd\ \left(6\right).\]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз).

При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Пример 1

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={\rm 2\ }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

Решение. Основой решения задачи является правило равновесия рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1.1\right),\]

где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:

\[\frac{m_1g}{m_2g}=\frac{d_2}{d_1}\to \frac{m_1}{m_2}=\frac{d_2}{d_1}\left(1.2\right).\]

Из выражения (1.2) получим искомую массу $m_1$:

\[m_1=\frac{m_2d_2}{d_1}.\]

Вычислим искомую массу:

\[m_1=2\cdot \frac{1}{4}=0,5\ (кг).\]

Ответ. $m_1=0,5\ кг$

Пример 2

Задание. Однородный стержень длинной $l\ $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $\alpha $. На стержне на расстоянии $b\ $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $M\overline{g}$, вес груза, расположенного на нем $\overline{P}=m_1\overline{g}$, сила реакции наклонной плоскости: $\overline{N}$; сила реакции опоры в точке A: $\overline{N}'$.

Плечи сил будем искать относительно точки A. Плечо силы $\overline{N'}$ будет равно нулю, так как сила приложена к стержню в точке А:

\[d_{N'}=0\ \left(2.1\right).\]

Плечо другой силы реакции опоры ($\overline{N}$) равно длине перпендикуляра AC:

\[d_N=l{\sin (90-\alpha )\ }=l{\cos \alpha \ \left(2.2\right).\ }\]

Плечо силы $M\overline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

\[d_{Mg}=\frac{l}{2}\left(2.3\right).\]

Плечо силы $m_1\overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:

\[d_{m_1g}=b.\]

Ответ. $d_{N'}=0;;\ d_N=l{sin (90-\alpha )\ }=l{cos \alpha \ \left(м\right),\ }d_{Mg}=\frac{l}{2},\ d_{m_1g}=b$

Читать дальше: формула полезной мощности.

}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.»,»word_count»:616,»direction»:»ltr»,»total_pages»:1,»rendered_pages»:1}

Источник: https://www.webmath.ru/poleznoe/fizika/fizika_137_formula_plecha_sily.php

Статья на ему

1 Расчеты рычажных механизмов

В результате проведения расчетов рычажного механизма необходимо определить размеры и взаимное расположение его звеньев, их кинематические параметры (скорость, ускорение), крутящий момент, приведенный к ведущему звену (кривошипному валу) обеспечивающий его работу в требуемом режиме и геометрические размеры его звеньев, позволяющие передавать возникающие при работе механизма усилия.

Методика выполнения кинематических и силовых расчетов рычажного механизма зависит от его типа, а прочностной расчет геометрических размеров входящих в него звеньев – от их конструктивного исполнения и направления сил и моментов, действующих на них. В общем, случае расчет рычажного механизма выполняется в следующей последовательности:

• расчет размеров (длин), определение исходного и конечного положения звеньев механизма, а также величину перемещения и траекторию движения его выходного звена,
• расчет скоростей и ускорений, возникающих в звеньях механизма,
• расчет усилий, в том числе инерционных, действующих на звенья механизма и потребного крутящего момента приведенного к ведущему звену,
• прочностной расчет звеньев механизма, (коленвал, шатун, ползун, шарниры),
• прочие расчеты, определяемые спецификой конструкции и работы механизма.

1.1 Расчет конструктивных параметров звеньев рычажных механизмов.

Расчет основных, конструктивных параметров механизма выполняется конструктором на первом этапе разработке (обычно на этапе эскизного проекта) и в значительной степени зависит от выбранного на этапе поиска технического решения типа механизма. Целью его проведения является нахождение линейных размеров звеньев механизма, определяющих его кинематику.

Кривошипно-коромысловый механизм

На Рис. 265 показана кинематическая схема кривошипно-коромыслового механизма.

При его проектировании обычно задается длина коромысла DC – b и угол его качения ψ, определяющий крайние положения выходного звена механизма, а также расстояние между осью А вращения кривошипа AB и осью D качания коромысла DC заданы, или определяются из конструктивных соображений, а расчетным путем необходимо определить плечо кривошипа r и длину шатуна l (см. Рис. 265а). Искомые размеры механизма рассчитываются на основании рассмотрения его крайних положений, показанных на Рис. 265б.

Кривошипно-ползунный механизм

На Рис. 266а показана кинематическая схема кривошипно-ползунного механизма.

При его проектировании обычно изначально заданы расстояние от плоскости перемещения ползуна до оси вращения кривошипа – e, расстояние от оси вращения кривошипа до оси соединения шатуна с ползуном при нахождении последнего в крайнем выдвинутом положении – H и ход ползуна – h, а определить необходимо радиус кривошипа – r и длину шатуна – l.

Искомые размеры механизма рассчитываются на основании рассмотрения его крайних положений, показанных на Рис. 266б.

Длина шатуна l определяется из рассмотрения

Источник: https://xn--80adfdbscmorebdjpezh9nvd.xn--p1ai/shop/product/raschetyi-mehanizmov/